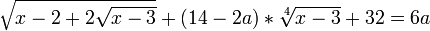Зовнішнє незалежне оцінювання 2012 року з математики (II сесія)
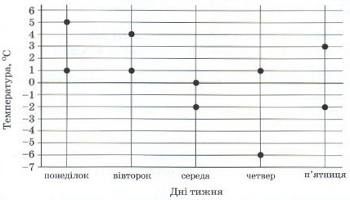
1. На рисунку показано жирними точками найвищу і найнижчу температури повітря кожного дня тижня з понеділка до п’ятниці в деякому місті України. По горизонталі відмічено дні тижня, а по вертикалі - температуру повітря в градусах Цельсія. У який день різниця між найвищою та найнижчою температурами повітря була найбільшою?
2. Протягом тижня два кур’єри разом доставили 210 пакетів. Кількості пакетів, доставлених першим і другим кур’єрами за цей період, відносяться як 3:7. Скільки пакетів доставив другий кур’єр?
3. Яка з наведених точок лежить у площині Oxz прямокутної системи координат у просторі?
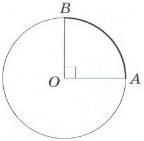
4. На рисунку зображено коло з центром в точці О, довжина якого дорівнює 64 см. Визначте довжину меншої дуги АВ кола, якщо ∠АОВ = 90°.
5. Використовуючи зображені на рисунку графіки функцій, розв’яжіть нерівність 2x > -х + 3.
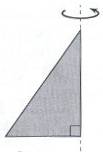
10. Прямокутний трикутник із катетами 9 см і 12 см обертається навколо більшого катета (див. рисунок). Визначте площу повної поверхні отриманого тіла обертання.
11. У магазині побутової техніки діє акція: на першу велику покупку (вартість перевищує 1000 грн) надається знижка 30 грн, на кожну наступну велику покупку попередня знижка збільшується на 25 грн. На яку за рахунком велику покупку отримає в цьому магазині покупець знижку 180 грн?
12. На рисунку зображено рівнобічну трапецію, бічна сторона якої дорівнює 2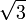
, а більша основа - 8. Визначте довжину діагоналі цієї трапеції, якщо її гострий кут дорівнює 30°.
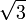, а більша основа - 8. Визначте довжину діагоналі цієї трапеції, якщо її гострий кут дорівнює 30°.
13. Порожній басейн, що вміщує х м3 води, повністю заповнюють водою за 5 годин (швидкість заповнення є сталою). За якою формулою можна обчислити кількість води V (у м3) у басейні через 2 години після початку його заповнення, якщо басейн був порожній і швидкість заповнення не змінювалась?
14. На рисунку зображено ромб, площа якого дорівнює 96 см2. У ромб вписано коло. Визначте площу зафарбованої фігури.
16. Висота правильної чотирикутної піраміди дорівнює 3 см, а бічне ребро - 5 см. Визначте косинус кута між бічним ребром і площиною основи.
Користувач не відповів на це запитання
20. Функція ƒ(x) в точці х0 = 5 має похідну ƒ'(5) = -1. Обчисліть значення похідної функції g(х)=ƒ(x)·x в точці x0, якщо ƒ(5) = 3.
21. До кожного виразу (1-4) доберіть тотожно рівний йому вираз (А- Д).
| 1. (а - 8) (а + 8) 2. (а - 8)2 3. (a - 4) (a2 + 4a +16) 4. (а - 4) (а-16) | А. а2 - 16a + 64 Б. а2 - 64 В. а2 - 20a + 64 Г. а3 + 64 Д. а3 - 64 |
22. Розв’яжіть рівняння (1 - 4). Установіть відповідність між кожним рівнянням та твердженням (А - Д), що є правильним для цього рівняння.
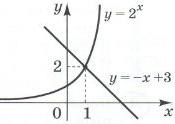
| 1. x + π = 0 2. cos x = 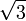 3. 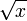 = 44. 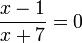 | А. коренем рівняння є ірраціональне число Б. коренем рівняння є число 16 В. рівняння не має коренів Г. рівняння має два корені Д. корінь рівняння належить відрізку [-2; 2] |
23. На рисунку зображено куб ABCDA1B1C1D1. Установіть відповідність між парою прямих та їхнім взаємним розміщенням.
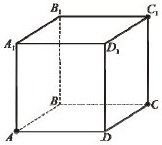
| 1. AC і CC1 2. AB1 і CD1 3. AC і CD1 4. AB1 і C1D | А. прямі паралельні Б. прямі мимобіжні В. прямі перетинаються і утворюють прямий кут Г. прямі перетинаються і утворюють кут 45° Д. прямі перетинаються і утворюють кут 60° |
24. На рисунку зображено графік функції y = ƒ(x), спадної на проміжку (-∞; +∞). Установіть відповідність між функцією (1-4) та точкою перетину її графіка з віссю Ох (А - Д).
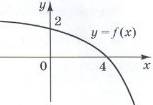
| 1. y = ƒ(x + 2) 2. y = ƒ(x - 2) 3. y = 2ƒ(x) 4. y = ƒ(x) - 2 | А. (0; 0) Б. (2; 0) В. (4; 0) Г. (6; 0) Д. (8; 0) |
25. Петро, Микола та Василь уранці відвідали кафе і кожен із них замовив собі на сніданок бутерброд та гарячий напій. Відомо, що Василь не п’є чорного чаю, а Микола замовив собі бутерброд із шинкою. Скориставшись таблицею, визначте, скільки грошей (у грн) буде коштувати Миколі, Василю і Петру разом найдешевше замовлення в цьому кафе.
| Страви | Ціна, грн |
| Бутерброд із сиром | 7.00 |
| Бутерброд із шинкою | 15.00 |
| Бутерброд із рибою | 17.00 |
| Кава з молоком | 13.00 |
| Кава | 12.00 |
| Чай чорний | 8.00 |
| Чай зелений | 9.00 |
26. Скільки всього різних двоцифрових чисел можна утворити з цифр 1, 5, 7 і 8 так, щоб у кожному числі всі цифри не повторювалися?
27. Розв’яжіть систему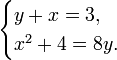 
Якщо пара (х0; y0) є єдиним розв’язком цієї системи рівнянь, то запишіть у відповідь добуток x0 · y0. Якщо пари (x1 ; y1) та (x2 ; y2) є розв’язками цієї системи рівнянь, то запишіть у відповідь найменший із добутків x1 · y1 та x2 · y2.
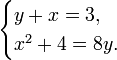Якщо пара (х0; y0) є єдиним розв’язком цієї системи рівнянь, то запишіть у відповідь добуток x0 · y0. Якщо пари (x1 ; y1) та (x2 ; y2) є розв’язками цієї системи рівнянь, то запишіть у відповідь найменший із добутків x1 · y1 та x2 · y2.
28. Бісектриса кута А прямокутника ABCD перетинає його більшу сторону ВС в точці М. Визначте радіус кола (у см), описаного навколо прямокутника, якщо ВС = 24 см, АМ = 10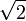 
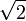см.
см.
.
30. Обчисліть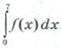 
, використовуючи зображений на рисунку графік лінійної функції y = ƒ(x).
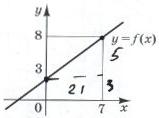
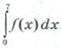, використовуючи зображений на рисунку графік лінійної функції y = ƒ(x).
31. Основою прямої призми ABCA1B1C1D1 є рівнобедрений трикутник АВС, де AB = BC =25 см, AC = 30 см. Через бічне ребро AA1 призми проведено площину, перпендикулярну до ребра BC. Визначте об’єм призми (у см3), якщо площа утвореного перерізу дорівнює 72 см2.
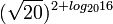