Зовнішнє незалежне оцінювання 2013 року з математики (I сесія)
4. Пряма b не має спільних точок з площиною а. Які з наведених тверджень є правильними?
I. Через пряму b можна провести лише одну площину, перпендикулярну до площини a.
II. Через пряму b можна провести лише одну площину, паралельну площині a.
III. У площині a можна провести лише одну пряму, паралельну прямій b.
I. Через пряму b можна провести лише одну площину, перпендикулярну до площини a.
II. Через пряму b можна провести лише одну площину, паралельну площині a.
III. У площині a можна провести лише одну пряму, паралельну прямій b.
6. На рисунку зображено графік функції у = ƒ(х), визначеної на проміжку [-5; 3]. Укажіть проміжок, на якому функція у = ƒ(х) зростає.


7. Розв’яжіть систему рівнянь 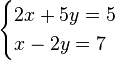 Для одержаного розв’язку (х0; у0) системи знайдіть суму х0 + у0.
Для одержаного розв’язку (х0; у0) системи знайдіть суму х0 + у0.
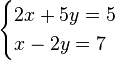 Для одержаного розв’язку (х0; у0) системи знайдіть суму х0 + у0.
Для одержаного розв’язку (х0; у0) системи знайдіть суму х0 + у0.
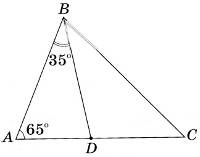
8. У трикутнику АВС: ∠А = 65°, BD - бісектриса кута В (див. рисунок). Знайдіть градусну міру кута ВСА, якщо ∠АВD = 35°.

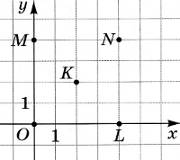
10. У координатній площині ху зображено п’ять точок: О, L, N, М, К (див. рисунок). Коло з центром в одній із цих точок дотикається до осі ординат у точці М. У якій точці знаходиться центр цього кола?

11. В арифметичній прогресії (аn) задано а1 = 4, а2 = -1. Укажіть формулу для знаходження n-го члена цієї прогресії.
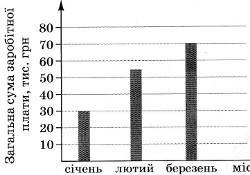
13. На діаграмі відображено нараховану фірмою загальну суму заробітної плати усім своїм працівникам у січні, лютому та березні 2011 року. У січні на фірмі працювали 15 співробітників, у лютому - 18, а в березні - 25. Як змінилася середня нарахована заробітна плата в цій фірмі в березні порівняно з січнем?

17. Менша сторона прямокутника дорівнює 16 м і утворює з його діагоналлю кут 60°. Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.
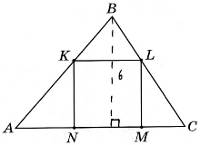
19. У трикутник АВС вписано квадрат KLMN (див. рисунок). Висота цього трикутника, проведена до сторони АС, дорівнює 6 см. Знайдіть периметр квадрата, якщо АС = 10 см.

20. Переріз кулі площиною має площу 81π см2. Знайдіть відстань від центра кулі до площини перерізу, якщо радіус кулі дорівнює 15 см.
21. Установіть відповідність між фігурою (1-4) і тілом обертання (А-Д), яке утворено внаслідок обертання цієї фігури навколо прямої, зображеної пунктиром.
1.  2.  3. 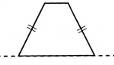 4. 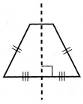 | А. 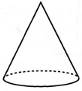 Б. 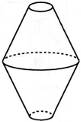 В. 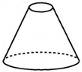 Г. 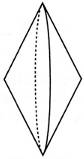 Д. 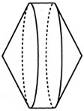 |
22. У прямокутній системі координат на площині ху задано точки О (0; 0) і А (6; 8). З точки А на вісь х опущено перпендикуляр. Точка В - основа цього перпендикуляра. Установіть відповідність між величиною (1-4) та її числовим значенням (А-Д).
| 1. ордината точки В 2. довжина вектора ОА 3. довжина радіуса кола, описаного навколо трикутника ОАВ 4. відстань від точки А до осі х | А. 0 Б. 5 В. 6 Г. 8 Д. 10 |
23. Дві однакові автоматичні лінії виготовляють 16 т шоколадної глазурі за 4 дні. Установіть відповідність між запитанням (1-4) та правильною відповіддю на нього (А-Д). Уважайте, що кожна лінія виготовляє однакову кількість глазурі щодня.
| 1. За скільки днів одна лінія виготовить 16 т шоколадної глазурі? 2. Скільки тонн шоколадної глазурі виготовить одна лінія за 2 дні? 3. Скільки таких ліній потрібно для виготовлення 48 т шоколадної глазурі за 4 дні? 4. Скільки тонн шоколадної глазурі дві лінії виготовляють за 3 дні? | А. 2 Б. 4 В. 6 Г. 8 Д. 12 |
24. На рисунку зображено графік функції у = ƒ(х), визначеної на проміжку [0; 11] та диференційовної на проміжку (0; 11). Установіть відповідність між числом (1-4) та проміжком (А-Д), якому належить це число.
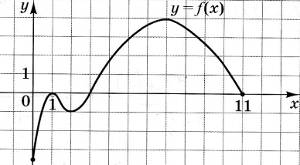

| 1. найменше значення функції у = ƒ(х) на її області визначення 2. 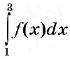 3. ƒ(8) 4. ƒ’(7) | А. (-∞; -2] Б. (-2; -0,5] В. (-0,5; 2] Г. (2; 4] Д. (4; +∞) |
25. Додатне число А більше додатного числа В у 3,8 раза. На скільки відсотків число А більше за число В?
27. Розв’яжіть нерівність 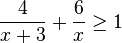 . У відповіді запишіть суму всіх цілих її розв’язків.
. У відповіді запишіть суму всіх цілих її розв’язків.
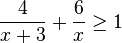 . У відповіді запишіть суму всіх цілих її розв’язків.
. У відповіді запишіть суму всіх цілих її розв’язків.
29. В автобусному парку налічується n автобусів, шосту частину яких було обладнано інформаційними табло. Пізніше інформаційні табло встановили ще на 5 автобусів з наявних у парку. Після проведеного переобладнання навмання вибирають один з n автобусів парку. Ймовірність того, що це буде автобус з інформаційним табло, становить 0,25. Визначте n. Уважайте, що кожен автобус обладнується лише одним табло.
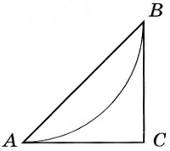
30. План паркової зони, обмеженої трикутником АВС, зображено на рисунку. Дуга АВ - велосипедна доріжка. Відомо, що дуга АВ є четвертою частиною кола радіуса 1,8 км. СА і СВ - дотичні до цього кола (А і В - точки дотику). Обчисліть площу зображеної на плані паркової зони (у км2).

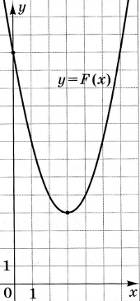
31. На рисунку зображено графік функції F(х) = х2 + bх + с, яка є первісною для функції ƒ(х). Визначте параметри b і с, знайдіть функцію ƒ(х). У відповіді запишіть значення ƒ(-8).

32. Основою піраміди SABCD є трапеція АВСD (АD||ВС), довжина середньої лінії якої дорівнює 5 см. Бічне ребро SВ перпендикулярне до площини основи піраміди і вдвічі більше від середньої лінії трапеції АВCD. Знайдіть відстань від середини ребра SD до площини SВС (у см), якщо об’єм піраміди дорівнює 210 см3.
33. Знайдіть значення параметра а, при якому корінь рівняння 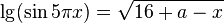 ) належить проміжку (3/2; 2)
) належить проміжку (3/2; 2)
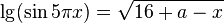 ) належить проміжку (3/2; 2)
) належить проміжку (3/2; 2)
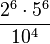
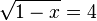
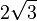 см.
см.
 =
=
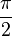 ; π).
; π).
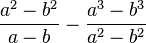 , якщо
, якщо