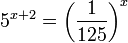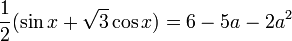Зовнішнє незалежне оцінювання 2011 року з математики
Користувач не відповів на це запитання
2. Учитель роздав учням певного класу 72 зошити. Кожен учень отримав однакову кількість зошитів. Якому з поданих нижче чисел може дорівнювати кількість учнів у цьому класі?
Користувач не відповів на це запитання
4. Укажіть лінійну функцію, графік якої паралельний вісі абсцис і проходить через точку A(-2; 3)
Користувач не відповів на це запитання
5. Доберіть таке закінчення речення, щоб утворилося правильне твердження: "Сума квадратів катетів прямокутного трикутника дорівнює..."
Користувач не відповів на це запитання
7. На рисунку зображено куб ABCDA1B1C1D1. Укажіть серед поданих нижче пряму, що утворює з СD1 пару мимобіжних прямих.
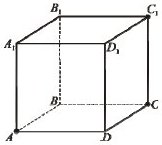
Користувач не відповів на це запитання
8. Журнал коштував 25 грн. Через два місяці цей самий журнал став коштувати 21 грн. На скільки відсотків знизилася ціна журналу?
Користувач не відповів на це запитання
9. На одиночному колі зображено точку P(-0.8; 0.6) і кут α (див. рисунок). Визначте cos α.
Користувач не відповів на це запитання
10. Знайдіть градусну міру внутрішнього кута правильного десятикутника.
Користувач не відповів на це запитання
11. Спростіть вираз a - |a|, якщо a < 0 .
Користувач не відповів на це запитання
12. Об’єм кулі дорівнює 36π см3. Знайдіть її діаметр.
Користувач не відповів на це запитання
13. Визначте знаменник геометричної прогресії bn,
якщо b9 = 24, b6 = -1/9
якщо b9 = 24, b6 = -1/9
Користувач не відповів на це запитання
15. Обчисліть площу чотирикутника ABCD (див. рисунок), сторони AB і CD якого паралельні вісі Oy
Користувач не відповів на це запитання
16. Якому з наведених проміжків належить корінь рівняння ?
Користувач не відповів на це запитання
17. На рисунку зображено коло з центром у точці O і рівносторонній трикутник АOB, що перетинає коло в точках M і N. Точка D належить колу. Знайдіть градусну міру кута MDN.
Користувач не відповів на це запитання
18. Функція y = ƒ(x) є спадною на проміжку (-∞;+∞). Укажіть правильну нерівність.
Користувач не відповів на це запитання
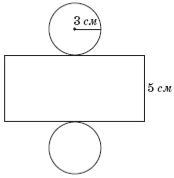
19. У прямокутник ABCD вписано три круги одного й того самого радіуса (див. рисунок). Визначте довжину сторони BC, якщо загальна площа кругів дорівнює 3π.
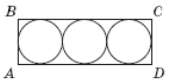
Користувач не відповів на це запитання
20. О шостій годині ранку визначено температуру на десяти метеостанціях. Отримані дані відображено в таблиці.
Визначте x, якщо середнє арифметичне всіх цих даних дорівнює 3.5°
Визначте x, якщо середнє арифметичне всіх цих даних дорівнює 3.5°
Користувач не відповів на це запитання
21. У трикутнику ABC: AB = 31 см, BC = 15 см, AC = 26 см. Пряма a, паралельна стороні AB, перетинає сторони BC і AC у точках M і N відповідно. Обчисліть периметр трикутника MNC, якщо MC = 5 см.
Користувач не відповів на це запитання
22. На рисунку зображено розгортку циліндра. Знайдіть його об’єм.
Користувач не відповів на це запитання
23. Розв’яжіть нерівність log0.5(x - 1) > 2.
Користувач не відповів на це запитання
24. Функція F(x) = 6 sin(2x) - 1 є первісною функції ƒ(x). Знайдіть функцію ƒ(x).
Користувач не відповів на це запитання
25. Діагональним перерізом правильної чотирикутної призми є прямокутник, площа якого дорівнює 40 см2. Периметр основи призми дорівнює 20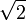
см. Визначтe висоту призми.
см. Визначтe висоту призми.
26. Установіть відповідність між функціями (1 – 4) та ескізами їхніх графіків (А – Д).
| Функція | Ескіз графіка функції |
|
1. y = tgx 2. y = ctgx 3. y =  4. y =
 |
А.  Б. 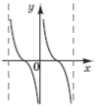 В. 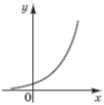 Г. 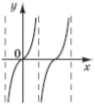 Д.  |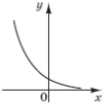
27. На рисунку зображено a, b, c, d. Установіть відповідність між парою векторів (1-4) і твердженням (А-Д), що є правильними для цієї пари.
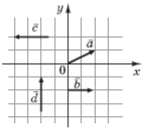
| Вектори | Твердження |
|
1. a і b 2. a і c 3. c і d 4. b і c |
А. вектори перпендикулярні Б. вектори колінеарні, але не рівні В. скалярний добуток векторів більший за 0 Г. вектори рівні Д. кут між векторами тупий |
28. Установіть відповідність між виразами (1 – 4), та їхніми значеннями якщо x=0.5 (А – Д).
| Вектори | Значення виразу |
|
1.  2. (x - 5)2 + 5(2x - 5) 3.  4.  |
А. -2.5 Б. -0.25 В. 0.25 Г. 1.5 Д. 2.5 |
30. Матеріальна точка рухається за законом s(t) = 2t2 + 3t, де s вимірюється в метрах, а t у секундах. Знайдіть значення t (у секундах), при якому миттєва швидкість матеріальної точки дорівнює 76 м/с.
31. У відділі працює певна кількість чоловіків і жінок. Для анкетування навмання вибрали одного із співробітників. Імовірність того, що це чоловік, дорівнює 
. Знайдіть відношення кількості жінок до кількості чоловіків, які працють у цьому відділі.
. Знайдіть відношення кількості жінок до кількості чоловіків, які працють у цьому відділі.
32. Двоє робітників, працюючи разом, можуть скосити траву на ділянці за 2 години 6 хвилин. Скільки часу (у годинах) витратить на скошування трави на цій ділянці другий робітник, працюючи самостійно, якщо йому потрібно на виконання цього завдання на 4 години більше ніж першому робітникові.
33. У чотирикутну піраміду, в основі якої лежить рівнобічна трапеція з бічною стороною 13 см і основами 18 см і 8 см, вписано конус. Знайдіть площу бічної поверхні конуса Sбічне (у см2), якщо всі бічні грані піраміди нахилені до площини основи під кутом 60°. У відповідь запишіть значення Sбічне/π
34. На рисунку зображено графік функції y = ƒ(x), що визначена на проміжку (-∞; +∞) і має лише три нулі.
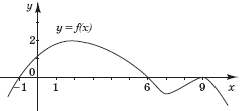
Розв’яжіть систему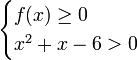
У відповідь запишіть суму всіх цілих розв’язків системи.
Розв’яжіть систему
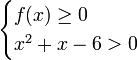
У відповідь запишіть суму всіх цілих розв’язків системи.
