Зовнішнє незалежне оцінювання 2014 року з математики
3. Які з наведених тверджень є правильними?
І. Сума двох будь-яких вертикальних кутів дорівнює 180°.
ІІ. Сума двох будь-яких суміжних кутів дорівнює 180°.
ІІІ. Сума будь-якого гострого кута та будь-якого тупого кута дорівнює 180°.
І. Сума двох будь-яких вертикальних кутів дорівнює 180°.
ІІ. Сума двох будь-яких суміжних кутів дорівнює 180°.
ІІІ. Сума будь-якого гострого кута та будь-якого тупого кута дорівнює 180°.
5. Арифметичну прогресію `a_n` задано формулою n-го члена `a_n = 4 - 8n` Знайдіть різницю цієї прогресії.
6. Вектор `\overrightarrow{OA}` лежить на осі z прямокутної декартової системи координат у просторі (див. малюнок), і його початок збігається з початком координат. Визначте координати вектора `\overrightarrow{OA}`, якщо його довжина дорівнює 3.

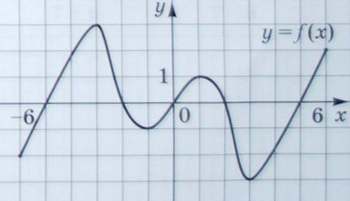
7. На малюнку зображено графік функції `y = f \big(x\big) `, яка визначена на проміжку [-6;6]. Яку властивість має функція `y = f \big(x\big)`?

8. Точка С лежить на осі x прямокутної системи координат і знаходиться на відстані 5 від точки A (-2; 4). Відрізок АС перетинає вісь y. Знайдіть координати точки С.
9. Студент на першому курсі повинен вибрати одну з трьох іноземних мов, яку вивчатиме, та одну з п’яти спортивних секцій, що відвідуватиме. Скільки всього існує варіантів вибору студентом іноземної мови та спортивної секції?
Користувач не відповів на це запитання
14. Розв’яжіть нерівність `(x + 4)^2 <= 16.`
Користувач не відповів на це запитання
15. У гострокутному трикутнику АВС проведена висота ВМ. Визначте довжину сторони АВ, якщо ВМ = 12, `\angle{A} = \alpha`
Користувач не відповів на це запитання
16. Відрізок АВ перетинає площину а в точці О. Проекція відрізків АО і ВО на цю площину дорівнює 5 см і 20 см відповідно. Знайдіть довжину відрізка АВ, якщо АО = 8 см.
Користувач не відповів на це запитання
17. Відомо, що `ctg(\alpha) < 0`, `\cos(\alpha) > 0`. Якого значення може набувати `sin(\alpha)`?
Користувач не відповів на це запитання
18. Укажіть рівняння дотичної, проведеної до графіка функції `y = f(x)` у точці з абсцисою `x_0 = 1`, якщо `f(x_0) = 5`, `f'(x_0) = 2`
Користувач не відповів на це запитання
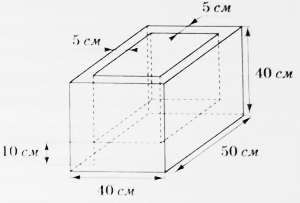
19. На площі міста встановили однакові бетонні ємності для квітів, виготовлені у формі прямокутних паралелепіпедів, виміри яких дорівнюють 40 см, 40 см і 50 см (див. рисунок). Товщина кожної з чотирьох бічних стінок становить 5 см, а товщина днища – 10 см. Який об’єм бетону (у метрах кубічних) було використано для виготовлення 10 таких ємностей? Утратою бетону під час виготовлення знехтуйте.

Користувач не відповів на це запитання
20. На рисунку зображено розгортку піраміди, що складається з квадрата, сторона якого дорівнює 10 см, і чотирьох правильних трикутників. Визначте площу бічної поверхні цієї піраміди (у `cm^2`)


21. До кожного виразу (1-4) доберіть тотожно йому рівний (А-Д), якщо `m>2`, `m` - натуральне число.
|
1. `(m + 1)^2 - m^2 - 1` 2. `m*cos^2(\alpha) + m*sin^2(\alpha)` 3. `100^{lg(m)}` 4. `log_{2}(\sqrt[m]{2})` |
А. 2m Б. 0 В. `1/m` Г. m Д. `m^2` |
22. Установіть відповідність між функцією (1-4) та кількістю спільних точок (А-Д) графіка цієї функції з графіком функції `y=x/5`:
|
1. `y=sin(x)` 2. `y=\sqrt(x)` 3. `y=5^x` 4. `y=x+5` |
А. жодної Б. лише одна В. лише дві Г. лише три Д. більше трьох |
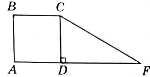
23. На рисунку зображено квадрат АВСD зі стороною 1 см та прямокутний трикутник СDF, гіпотенуза якого CF дорівнює `\sqrt{3}` см. Фігури лежать в одній площині. Установіть відповідність між початком речення (1-4) та його закінченням (А-Д) так, щоб утворилося правильне твердження.

|
1. Довжина катета FD трикутника СВF дорівнює 2. Довжина радіуса кола, описаного навколо квадрата АВСD, дорівнює 3. Відстань від точки F до прямої ВС дорівнює 4. Відстань від точки F до прямої BD дорівнює |
А. `\sqrt{5}` см. Б. `\sqrt{2}` см. В. 2 см. Г. 1 см. Д. `1/\sqrt{2}` см. |
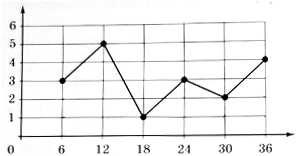
24. На малюнку зображений полігон частот деякого ряду даних. По осі абсцис відзначені елементи цього ряду, а по осі ординат їх частоти. Установіть відповідність між характеристикою (1-4) цього ряду даних та її числовим значенням (А-Д).

|
1. мода 2. медіана 3. кількість елементів 4. розмах |
А. 12 Б. 18 В. 21 Г. 30 Д. 36 |
25. Початкова вартість сукні становила 144 грн. В результаті уцінки вартість цього плаття зменшилася на 80%.
Обчисліть вартість плаття після уцінки (у грн).
Обчисліть вартість плаття після уцінки (у грн).
26. Початкова вартість сукні становила 144 грн. В результаті уцінки вартість цього плаття зменшилася на 80%.
Скільки відсотків становить початкова вартість сукні від її вартості після уцінення?
Скільки відсотків становить початкова вартість сукні від її вартості після уцінення?
27. На стороні AD паралелограма ABCD як на діаметрі побудована півколо так, що воно дотикається до сторони BC в точці М. Довжина дуги МD дорівнює `8.5*\pi` см.
Обчисліть довжину радіуса цього півкола (в см)
Обчисліть довжину радіуса цього півкола (в см)
28. На стороні AD паралелограма ABCD як на діаметрі побудована півколо так, що воно дотикається до сторони BC в точці М. Довжина дуги МD дорівнює `8.5*\pi` см.
Обчисліть площу паралелограма ABCD (в `cm^2`)
Обчисліть площу паралелограма ABCD (в `cm^2`)
29. Відомо, що `(y-x)/(2x)=7/4`, де `0 < x < y`. У скільки разів число `y` більше числа `x`?
30. Вартість Р (у грн.) поїздки на таксі обчислюють за формулою:
`P = \begin{cases} P_{min}+2.4*(S-6)+0.5*t & , S>6 \\ P_{min} & , S<6 \end{cases} `,
де S - відстань (у км), яку проїхало таксі під час поїздки, `P_{min}` - мінімальна вартість поїздки (у грн), t - час (у хв.), протягом якого швидкість таксі не перевищула 5 км/год. Користуючись формулою, обчисліть вартість поїздки (у грн) на таксі, якщо S = 12,5 км, `P_{min}` = 28 грн, t = 12 хв.
31. Розв'яжіть рівняння `log_{0.4}(5x^2 - 9) = log_{0.4}(-4x)`. Якщо рівняння має єдиний корінь, запишіть його у відповіді. Якщо рівняння має кілька коренів, запишіть у відповіді їхню суму.
32. Розв'яжіть нерівність `(10^x-16*5^x)/(x+2) \geq 0`. У відповіді запишіть суму всіх цілих розв'язків нерівності на проміжку [-3;6].
33. Діагональ рівнобічної трапеції є бісектрисою її гострого кута і ділить середню лінію трапеції на відрізки довжиною 15 см і 33 см. Обчисліть (у `cm^2`) площу трапеції.
34. На рисунку зображено ескіз графіка квадратичної функції `f(x)=ax^2+(2bx)/3+5`. Площа криволінійної трапеції, обмеженої лініями y=f(x), y=0, x=1, дорівнює 19 кв. од. Обчисліть суму a+b.


35. Через точки А і В, що лежать на колах верхньої та нижньої основ циліндра і не належать одній твірній, проведено площину паралельно осі циліндра. Відстань від центра нижньої основи до цієї площини дорівнює `\sqrt{10}`, а площа утвореного перерізу становить `54*\sqrt{10}`. Визначте довжину відрізка АВ (у см), якщо площа бічної поверхні циліндра дорівнює `180*\pi \thinspace cm^2`.
36. Знайдіть усі від'ємні значення параметра
`P =\begin{cases} 2*\sqrt{y^2-4y+4}+3|x| = 17-y \\ 25x^2-20ax=y^2-4a^2 \end{cases} `,
при яких система рівнянь , має єдиний розв'язок. Якщо таке значення одне, то запишіть його у відповіді. Якщо таких значень кілька, то у відповіді запишіть їхню суму.