Зовнішнє незалежне оцінювання 2012 року з математики (I сесія)
1. Два кола з центрами в точках О і О1 мають внутрішній дотик (див. рисунок). Обчисліть відстань ОО1 якщо радіуси кіл дорівнюють 12 см і 8 см.
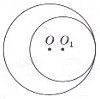

3. На діаграмі відображено кількість відвідувачів Музею Води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніж у попередній день?
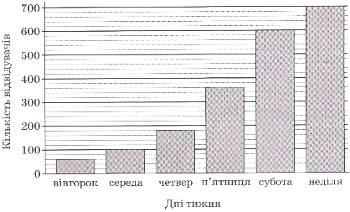

4. Яка з наведених точок належить осі Оz прямокутної системи координат у просторі?
5. На рисунку зображено графік функції у = ƒ(x), визначеної на проміжку [-4; 4]. Знайдіть множину всіх значень x для яких ƒ(x) ≤ -2.
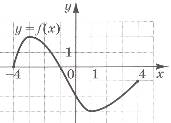

6. Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 5000 грн, розподіливши гроші таким чином: перший отримав четверту частину зароблених грошей, а другий - решту. Скільки гривень отримав за цю роботу другий фахівець?
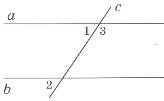
7. Пряма c перетинає паралельні прямі a і b (див. рисунок). Які з наведених тверджень є правильними для кутів 1, 2, З?
I. ∠1 і ∠3 - суміжні.
II.∠1 = ∠2.
III. ∠2 + ∠3 = 180°.
I. ∠1 і ∠3 - суміжні.
II.∠1 = ∠2.
III. ∠2 + ∠3 = 180°.

Користувач не відповів на це запитання
9. При якому значенні x вектори a(2; x) і b(-4; 10) перпендикулярні?
10. На якому з наведених рисунків зображено ескіз графіка функції
у = 4 - (х - 1)^2?
у = 4 - (х - 1)^2?
11. У залі кінотеатру 18 рядів. У першому ряду знаходяться 7 місць, а в кожному наступному ряду на 2 місця більше, ніж у попередньому. Скільки всього місць у цьому залі?
12. Прямокутник із сторонами 8 см і 10 см обертається навколо меншої сторони (див. рисунок). Знайдіть площу повної поверхні отриманого тіла обертання.


14. З міст А і B, відстань між якими по шосе становить 340 км, одночасно назустріч один одному виїхали автобус і маршрутне таксі зі сталими швидкостями 65 км/год і 80 км/год відповідно. Автобус і маршрутне таксі рухаються без зупинок і ще не зустрілися. За якою формулою можна обчислити відстань S (у км) між автобусом і маршрутним таксі по шосе черев t годин після початку руху?
15. Висота правильної чотирикутної піраміди дорівнює 4 см, а її апофема - 5 см. Визначте косинус кута між площиною бічної грані піраміди і площиною основи.
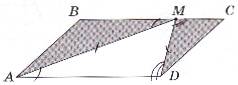
16. На рисунку зображено паралелограм ABCD, площа якою дорівнює 60 см2. Точка М належить стороні BC. Визначте площу фігури, що складається з двох зафарбованих трикутників.

18. У прямокутнику ABCD: ВС = 80, АС = 100. Через точки M і K, що належать сторонам АВ і ВС відповідно, проведено пряму, паралельну АС. Знайдіть довжину більшої сторони трикутника МВК якщо ВК = 20.
19. Укажіть множину всіх значень а, при яких виконується рівність
|a3 - a2| = a3 - a2
|a3 - a2| = a3 - a2
20. Функція ƒ(x) має в точці x0 похідну ƒ '(x0) = -4. Визначте значення похідної функції g(х) = 2 · ƒ(x) + 7x - 3 в точці x0.
21. До кожного виразу (1 - 4) при а > 0, доберіть тотожно йому рівний (А - Д).
1. 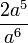 2. (2a)5 · a6 3. (2a6)5 4.
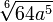 |
А. 32a11 Б. 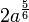 В. 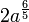 Г. 2a-1 Д. 32a30 |
22. Кожній точці (1 - 4) поставте у відповідність функцію (А - Д), графіку якої належить ця точка.
|
1. O(0; 0) 2. М(0; -1) 3. N(-1; 0) 4. K(0; 1) |
А. у = 2х + 2 Б. у = ctgx В. у = tgx Г. у = √x - 1 Д. у = 2x |
23. Розв’яжіть рівняння (1-4). Установіть відповідність між кожним рівнянням та кількістю його коренів (А - Д) на відрізку [-5; 5].
| Рівняння | Кількість коренів на відрізку [-5; 5] |
|
1. cos2x - sin2x = 1 2. log3x = -2 3. 4. x4 + 5x2 +4 = 0 |
А. жодного Б. один В. два Г. три Д. чотири |
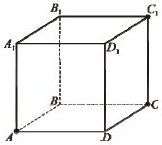
24. На рисунку зображено куб ABCDA1B1C1D1. До кожного початку речення (1 - 4) доберіть його закінчення (А - Д) так, щоб утворилося правильне твердження.

| Початок речення | Закінчення речення |
|
1. Пряма СВ 2. Пряма CD1 3. Пряма АС 4. Пряма A1B |
А. паралельна площині АА1В1В. Б. перпендикулярна площині АА1В1В. В. належить площині АА1В1В. Г. має з площиною АА1В1В лише дві спільні точки. Д. утворює з площиною АА1В1В кут 45°. |
25. Батьки разом із двома дітьми: Марійкою (4 роки) та Богданом (7 років) - збираються провести вихідний день у парку атракціонів. Батьки дозволяють кожній дитині відвідати не більше трьох атракціонів і кожний атракціон - лише по одному разу. Відомо, що на атракціони «Електричні машинки» і «Веселі гірки» допускають лише дітей старше 6 років. На «Паровозик» Богдан не піде. Для відвідування будь-якого атракціону необхідно купити квиток для кожної дитини. Скориставшись таблицею, визначте максимальну суму коштів (у грн), що витратять батьки на придбання квитків для дітей.
| Назва атракціону | Вартість 1 квитка для 1 дитини, грн |
| Веселі гірки | 17 |
| Паровозик | 16 |
| Електричні машинки | 20 |
| Карусель | 12 |
| Батут | 15 |
| Дитяча рибалка | 8 |
| Лебеді | 13 |
26. Скільки існує різних дробів 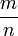 , якщо m набуває значень 1; 2 або 4, а n набуває значень 5; 7; 11; 13 або 17?
, якщо m набуває значень 1; 2 або 4, а n набуває значень 5; 7; 11; 13 або 17?
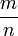 , якщо m набуває значень 1; 2 або 4, а n набуває значень 5; 7; 11; 13 або 17?
, якщо m набуває значень 1; 2 або 4, а n набуває значень 5; 7; 11; 13 або 17?
27. Розв’яжіть систему рівнянь 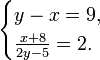 Запишіть у відповідь добуток x0 · y0, якщо пара (x0; y0) є розв’язком цієї системи рівнянь.
Запишіть у відповідь добуток x0 · y0, якщо пара (x0; y0) є розв’язком цієї системи рівнянь.
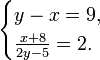 Запишіть у відповідь добуток x0 · y0, якщо пара (x0; y0) є розв’язком цієї системи рівнянь.
Запишіть у відповідь добуток x0 · y0, якщо пара (x0; y0) є розв’язком цієї системи рівнянь.
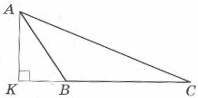
29. У трикутнику АВС основа висоти АК лежить на продовженні сторони ВС (див. рисунок). АК = 6, КВ = 2√3. Радіус описаного навколо трикутника АВС кола дорівнює 15√3. Визначте довжину АС.

30. Обчисліть 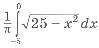 , використовуючи рівняння кола x2 + y2 = 25, зображеного на рисунку.
, використовуючи рівняння кола x2 + y2 = 25, зображеного на рисунку.
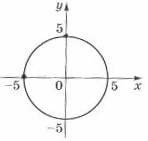
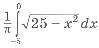 , використовуючи рівняння кола x2 + y2 = 25, зображеного на рисунку.
, використовуючи рівняння кола x2 + y2 = 25, зображеного на рисунку.
31. Основою прямої призми ABCDA1B1C1D1 є рівнобічна трапеція АВСD. Основа AD трапеції дорівнює висоті трапеції і в шість разів більша за основу ВС. Через бічне ребро CC1 призми проведено площину паралельно ребру АВ. Знайдіть площу утвореного перерізу (у см2), якщо об’єм призми дорівнює 672 см3, а її висота 8 см.
32. При якому найменшому цілому значенні
параметра а рівняння
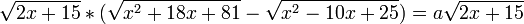 має лише два різні корені?
має лише два різні корені?
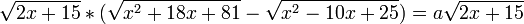 має лише два різні корені?
має лише два різні корені?

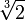 ,
, 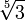 в порядку зростання.
в порядку зростання.
 .
.